

Lets start with deriving Tsiolkovsky's Rocket equation.
A rocket has mass m. That's the total mass, hull, payload, fuel tanks, fuel and engines.
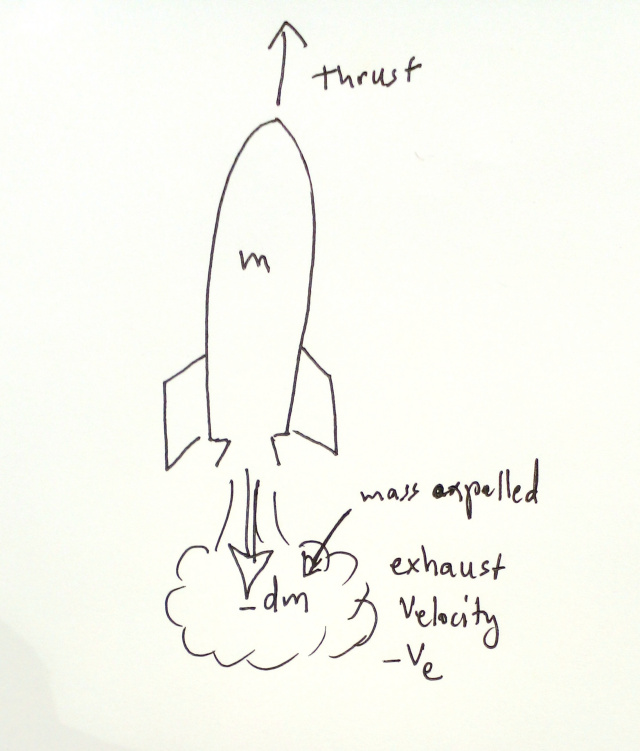
Now ignite the engines. At every instant dt, a small amount of mass dm is expelled out the exhaust nozzle. Follow me? We give dm a negative sign because it's removing mass from the rocket.
The mass is traveling backwards at the exhaust velocity Ve. This velocity is negative because it's pointing backwards.
The momentum is $$ (-V_e)(-dm) $$.
The rate of change of momentum per time dt is thus
$$ V_e \frac{dm}{dt} $$
According to Newton's Third Law, for every action, there is an equal and opposite reaction. The negative sign will reappear.
Thrust F = ma
$$ ma = m \frac{dv}{dt} = - V_e \frac{dm}{dt} $$
Simplifying this by multiplying out dt (Pure mathematicians will have a fit!)
$$ m dv = - V_e dm $$
We can rearrange and integrate.
The rocket will be at initial velocity v1 and its final velocity will be v2. The mass of the rocket starts as m1, and after burning fuel for a while will be m2.
$$\int_{v_1}^{v_2} dv = -V_e \int_{m_1}^{m_2} \frac{1}{m} dm $$
$$ v_2 - v_1 = \Delta v = V_e log\left(\frac{m_1}{m_2}\right) $$
Note that m1 is rocket plus fuel, while m2 is rocket minus fuel burned to get velocity v2.
So this is Tsiolkovsky's Rocket Equation. We will examine its implications on another page.