How did astronomers calculate the distances to planets even before radar? They measured the angles between a planet and a star. It's amazing what you can do just by measuring angles and some basic trigonometry.
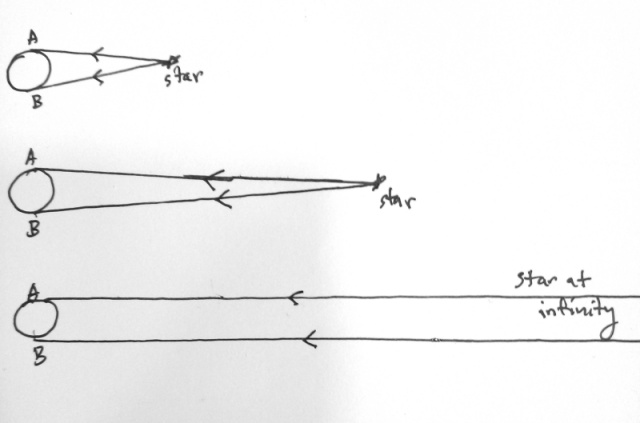
But first, we need to look at how two observers perceive rays of light from a distant star. If an object is close to the observers, the rays of light traveling to each observer makes an angle. But the further away the object is, the smaller the angle.
If the object is infinitely far away, the rays reaching each observer can be considered to be parallel. See the Figure below

This will simplify the parallax calculations below.
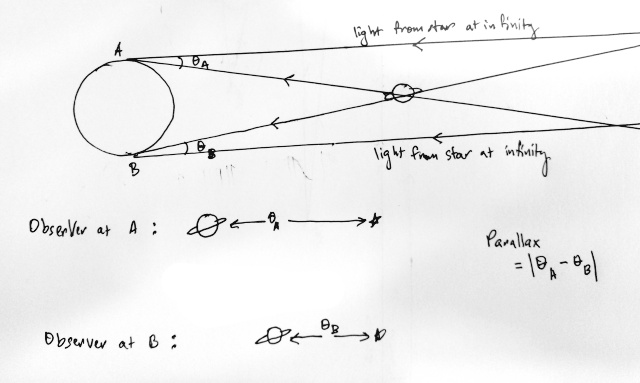
The angle between a star and a planet changes depending on the location of the astronomer.
Parallax can be described as... well, if there is an object close to you, it appears to be in front of something in the distance, but if you move sideways, it is no longer in front of that distant thing. When applied to astronomy, if you observe a planet to be in front of a star, someone on the other side of the Earth would see that planet to be one side of the star.
The Figure below assumes a star is at infinity, to show how a planet might seem "closer" to a star or "further" away, depending on an observer's position on Earth. The apparent shift of a planet's position is called the parallax angle.
 Hmmm... I think this is not correct. I'll have to reconsider this figure.
Hmmm... I think this is not correct. I'll have to reconsider this figure.
Using trigonometry:
$$ \tan \frac{\theta}{2} =\frac{R}{D}$$ $$ D = \frac{R}{ \tan \frac{\theta}{2}} $$Where D is the distance between Earth and the planet, d is the diameter of the Earth, which is the distance between the observers at A and B, \(\theta\) is the parallax angle. R is the radius of Earth, which is half of the diameter.
Things are a bit more complicated than that, of course. The planets are pretty far, and the angles involved are really small. For Jupiter, let us say for an example parallax angle is about 0.004 degrees, depending on its position in orbit. The radius R of Earth is 6371 km or \(6.37 \times 10^{6}\) m.
So $$ D = \frac{R}{\tan \frac{\theta}{2}} = \frac{6371 }{\tan \frac{0.004}{2}} km $$ This gives us D = 91,257,852 km
Distances to other planets can be determined in a similar way. Each of them will have different values of parallax angle (and since Earth and the planets are all moving, the parallax angle changes). We can determine the distances to the planets.
But these days they use radar or bounce laser light off the planets. But it was possible even before lasers and radar to determine the distances to the planets.