
Measuring the distance of planets
Now we can just use radar and bounce radio waves off a planet to measure how far away a planet is. But it has been possible for centuries, long before the invention of radar, to measure the distance to another planet.
The key is to measure the angular separation between a planet and a star. If another observer far away, ideally on the other side of the Earth, makes the same measurement, he will notice a difference, due to something called parallax.
Parallax is one of those things that is hard for me to explain just using words. You really need a picture or a figure. As you can see below, one observer sees the tree as being in front of the mountain, while the other observer in a different position sees it as being to one side of the mountain. This is a demonstration of parallax.

Similarly, two observers looking at the same planet will see its position is not the same with a star in the distant background. The star is so much further away that it can be considered to be at infinity, which will simplify calculations we will make.

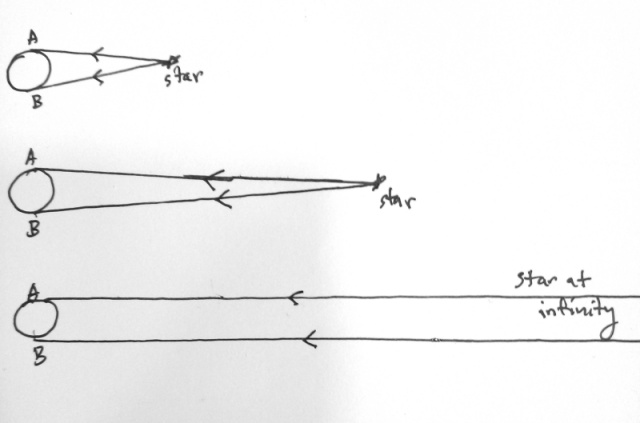
In the old days it was hard to get a second observer on the other side of the Earth. What they actually did was make an observation, measuring the angle between a planet and a star, then wait 12 hours so that the rotation of the Earth will take them to the opposite side, then make the second measurement.
Adding the two different angles gives you the Parallax Angle. The Figure below shows the geometry of this.
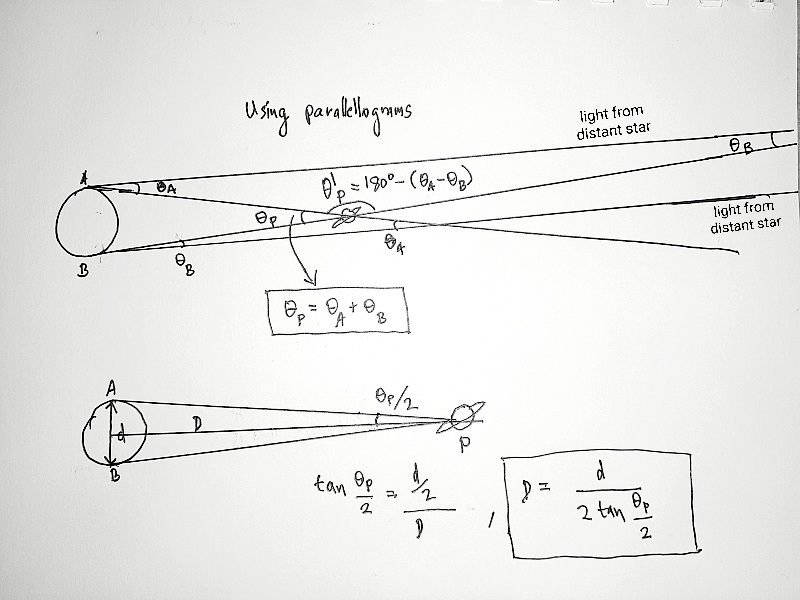
The next step is some simple trigonometry.
If d is the distance between two observers, D is the distance to a planet, and theta_P the parallax angle, then
$$ \tan \frac{\theta}{2} = \frac{d}{2D} $$
Rearranging, distance D to the planet is given by
$$ D = \frac{d}{2 \tan \frac{\theta}{2}} $$
So what you'd do is:
$$ D = \frac{d}{2 \tan \frac{\theta}{2}} $$
So for an example, we will calculate the distance to planet Jupiter.
For Jupiter, let us say for an example parallax angle is about 0.004 degrees, depending on its position in orbit. The radius R of Earth is 6371 km. Remembering that R = d/2.
$$ D = \frac{R}{ \tan \frac{\theta}{2}} $$
$$ D = \frac{6371}{ \tan \frac{0.004}{2}} $$
This gives us D = 91,257,852 km
Distances to other planets can be determined in a similar way. Each of them will have different values of parallax angle (and since Earth and the planets are all moving, their distances and thus parallax angles change too). We can determine the distances to the planets.
It was this careful, painstaking repeated measurements of positions and distances of planets at different times of year, every night that enabled Kepler to arrive at the Laws of Planetary Motion. Although, he did it mostly with Mars rather than Jupiter. He plotted how the distance changed night after night. The way the planets move closer, then further from Earth, showed all planets were orbiting the Sun, and furthermore, they moved in nearly circular ellipses.
This page shows how the movements of Earth and Mars change their distances from each other.
Earth Mars Distance, a VPython/GlowScript program.
This program was written in VPython, which GlowScript converts into JavaScript to run on browsers.
My source code on GlowScript:
https://www.glowscript.org/#/user/zorniy/folder/Physics/program/EarthMarsDistance/edit